
The efficiency of the proposed control chart is shown over the S^2 control chart designed under the classical statistics in neutrosophic average run length (NARL). Some tables are given for the practical use. The neutrosophic coefficient of S^2 control chart will be determined through the neutrosophic algorithm. The necessary measures of neutrosophic S^2 will be given. The complete structure of the neutrosophic S^2 control chart will be given. In this paper, we will originally design S^2 control chart under the neutrosophic interval methods. The neutrosophic statistics which is the extension of the classical statistics has been widely used when there is uncertainty in the data. The existing variance control charts are designed under the assumptions that no uncertain, fuzzy and imprecise observations or parameters in the population or the sample. The analyses suggest that the IT2F-SCUSUM chart is a promising tool in examining conformance of the quality of the fertilizer production. Thus, we can conclude that the IT2F-SCUSUM chart is more sensitive and takes lesser number of observations to identify the shift in the process. In the analysis of average run length, the proposed IT2F-SCUSUM chart outperforms the other two CUSUM charts. The conventional chart shows that 13 samples are “out of control.” In contrast, the type-1 fuzzy CUSUM chart shows that the process is “out of control” for 14 samples. The proposed IT2F-SCUSUM control chart unveils that 15 samples are “out of control.” The results are also compared to the conventional CUSUM chart and type-1 fuzzy CUSUM chart. Twenty samples with a sample size of six were examined for testing the conformance. This new approach combines the advantages of interval type-2 fuzzy numbers and standardized sample means which can control the variability. In this paper, we develop an interval type-2 fuzzy standardized cumulative sum (IT2F-SCUSUM) control chart and apply it to data of fertilizer production.
Nevertheless, some of the data used are more suitable to be presented in interval type-2 fuzzy numbers compared to type-1 fuzzy numbers as interval type-2 fuzzy numbers have more ability to capture uncertain and vague information. Previous literature suggests that fuzzy charts are more sensitive than conventional control charts, and hence, they provide better quality and conformance of products. Control chart is one of the powerful tools of statistical process control that are used to control nonconforming products. Now you want to examine the same data using an individuals and moving range chart.Statistical process control is a method used for controlling processes in which causes of variations and correction actions can be observed. You previously created a Moving Average chart. Each batch should weigh approximately 930 pounds. You can also estimate σ using the median of the moving range, change the length of the moving range, or enter aĪs the distribution manager at a limestone quarry, you want to monitor the weight (in pounds) and variation in the 45 batches of limestone that are shipped weekly to an important client. The moving range is of length 2, since consecutive values have the greatest chance of being alike.
#MINITAB I MR CHART HOW TO#
See for a discussion of how to interpret joint patterns in the two charts.īy default, I-MR Chart estimates the process variation, σ, with MRbar / d2, the average of the moving range divided by an unbiasing constant. Seeing both charts together allows you to track both the process level and process variation at the same time, as well as detect the presence of special causes. The Individuals chart is drawn in the upper half of the screen the Moving Range chart in the lower half.
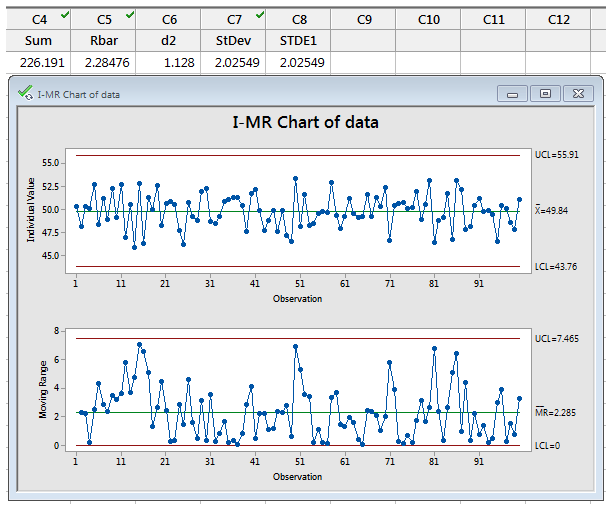
Moving Range − a chart of moving rangesĪn I-MR chart is an Individuals chart and Moving Range chart in the same graph window.Individuals − a chart of individual observations.Z-MR − a chart of standardized individual observations and moving ranges from short run processes.I-MR − an Individuals chart and Moving Range chart displayed in one window.Minitab offers five variables control charts: Variables control charts for subgroups, time-weighted charts, and multivariate charts also plot measurement data.Īttributes control charts plot count data, such as the number of defects or defective units.įor more information about control charts, see Control Charts Overview.Ĭhoosing a variables control chart for individuals Variables control charts for individuals plot statistics from measurement data, such as length or pressure, for individuals data.


 0 kommentar(er)
0 kommentar(er)
